论文笔记:Deep Closest Point: Learning Representations for Point Cloud Registration
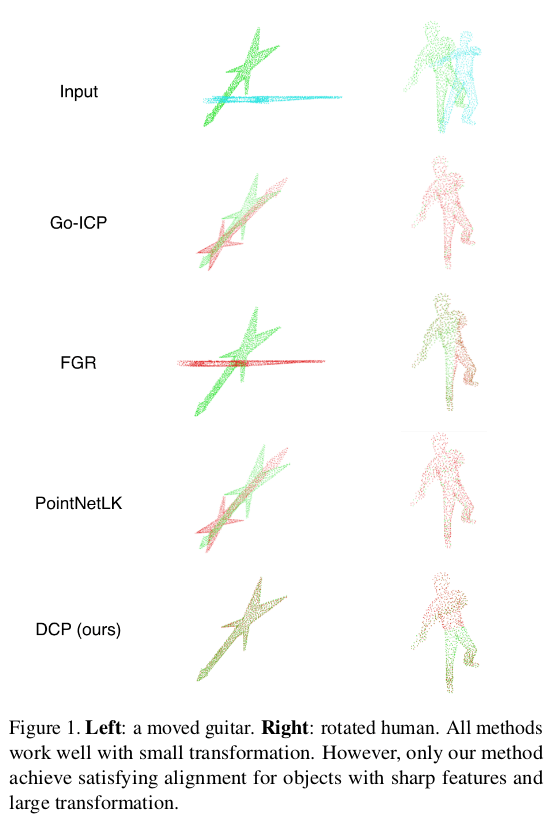
DCP 是一篇基于 Deep Learning 来解决 ICP 问题的,其中 Deep Learning 部分主要用于做匹配,后端仍然沿用 SVD 的方法。比很多 MLP 直接出 Pose 的合理,也取得了更好的效果。在与传统方法例如 Go-ICP 以及深度学习方法 PointNetLK 的对比中,都取得了一定的优势。
1 经典 ICP 问题
这一部分在之前的论文笔记中已经有了比较详细的阐述,参见:使用 SVD 方法求解 ICP 问题。
2 Deep Closest Point
参照经典的使用 SVD 求解 ICP 问题的流程,我们采用神经网络提取特征,并且使用注意力机制,最终使用一个可导 SVD layer 进行求解(在 PyTorch 和 Tensorflow 都提供了这样的 Layer)。整体网络结构框架如下图所示:
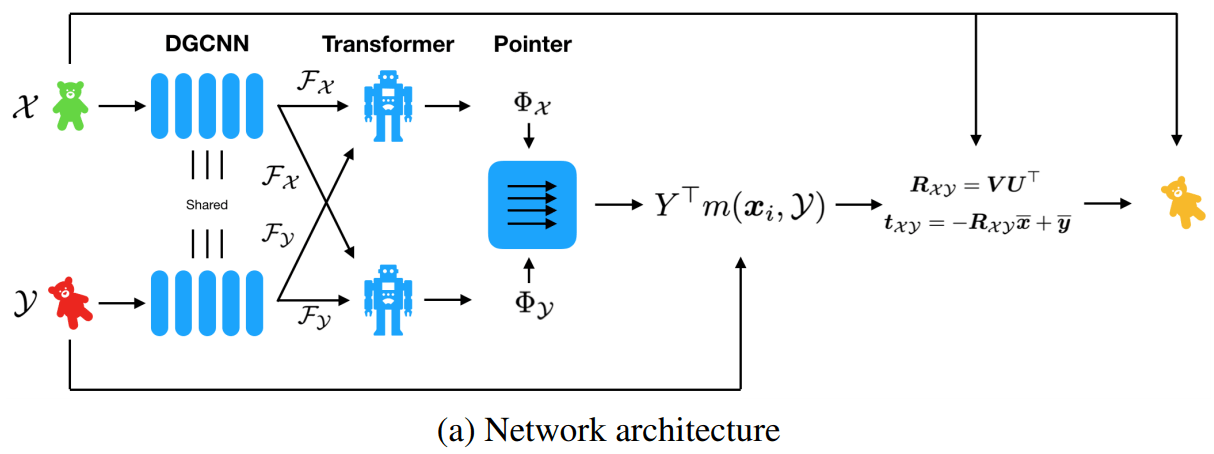
2.1 特征提取
我们定义点云 \(\mathcal{X}=\{\boldsymbol{x}_{1},\ldots,\boldsymbol{x}_{i},\ldots,\boldsymbol{x}_{N}\}\subset\mathbb{R}^{3}\) 和 \(\mathcal{Y}=\{\boldsymbol{y}_{1},\ldots,\boldsymbol{y}_{j},\ldots,\boldsymbol{y}_{M}\}\subset\mathbb{R}^{3}\) 是需要匹配的两对点云,为简便直接考虑 M=N 的情况。定义在网络最后一层之前(第 L 层)提取的局部特征分别为 \(\mathcal{F}_{\mathcal{X}}=\{\boldsymbol{x}_{1}^{L},\boldsymbol{x}_{2}^{L},...,\boldsymbol{x}_{i}^{L},...,\boldsymbol{x}_{N}^{L}\}\) 和 \(\mathcal{F}_{\mathcal{Y}}=\{\boldsymbol{y}_{1}^{L},\boldsymbol{y}_{2}^{L},...,\boldsymbol{y}_{i}^{L},...,\boldsymbol{y}_{N}^{L}\}\)。
在点云特征提取部分,作者分析了两个网络,一种是 PointNet,一种是 DGCNN(当然 DCP 作者也是 DGCNN 作者自然要分析自己的)。这一部分参见:论文笔记:Dynamic Graph CNN for Learning on Point Clouds,已经对二者的区别进行了分析。简单说就是 PointNet 对于每个点进行独立的特征提取没有考虑点和周围点的关系,而 DGCNN 使用 knn 把邻域的信息包含了进来,更符合特征提取的要求,也会取得更好的匹配结果。
2.2 注意力机制
本文的 Embeding 和 Attentation 都是借鉴了 NLP 领域的一些概念。
Embeding
Embeding 可以简单理解为将一个数据映射到另一个空间形成新的表达。本文将 2.1 中 \(\mathcal{F}_{\mathcal{X}}\) 和 \(\mathcal{F}_{\mathcal{Y}}\) 看做相对于原始点云的 Embeding,其实也就是每个点相对位置的特征。
Attention
本文的注意力模型是学习一个函数:\(\phi:\mathbb{R}^{N\times P}\times\mathbb{R}^{N\times P}\to\mathbb{R}^{N\times P}\),其中 N 是代表点的数量,P 是代表 Embeding 也就是特征的维度。也就是说通过函数 对原始点云的特征进行加权转换后求得一个新的 Embeding,这个 Embding 是由 \(\mathcal{F}_{\mathcal{X}}\) 和 \(\mathcal{F}_{\mathcal{Y}}\) 获得,可以理解为是基于两个点云的匹配关系对 Embeding 进行加入 Attention 的重新生成新的 Embeding,其表达式如下:
\(\begin{aligned} \Phi_{\mathcal{X}} &=\mathcal{F}_{\mathcal{X}}+\phi\left(\mathcal{F}_{\mathcal{X}}, \mathcal{F}_{\mathcal{Y}}\right) \\ \Phi_{\mathcal{Y}} &=\mathcal{F}_{\mathcal{Y}}+\phi\left(\mathcal{F}_{\mathcal{Y}}, \mathcal{F}_{\mathcal{X}}\right) \tag{1}\end{aligned}\)这里面,我们将函数 \(\phi\) 看做是一个残差,通过由 \(\mathcal{F}_{\mathcal{X}}\) 和 \(\mathcal{F}_{\mathcal{Y}}\) 学习到的关系,对于原有的 Embeding 进行的改变。这里的逻辑是,通过这样的映射 \(\mathcal{F}_{\mathcal{X}}\mapsto\Phi_{\mathcal{X}}\),\(\Phi_{\mathcal{X}}\) 不仅包含了原始点云 \(\mathcal{X}\) 的特征,同时也包含了目标点云 \(\mathcal{Y}\) 中结构的知识,因此对于我们所要进行的点云配准任务是更加有利的。反之同理。
这里面的函数 \(\phi\) 本文借鉴 NLP 中的 Transformer 网络来实现,因为点云匹配很像是一个 sep2seq 的问题,因而可以用这样的方式来处理。Transformer 的结构如下图所示:
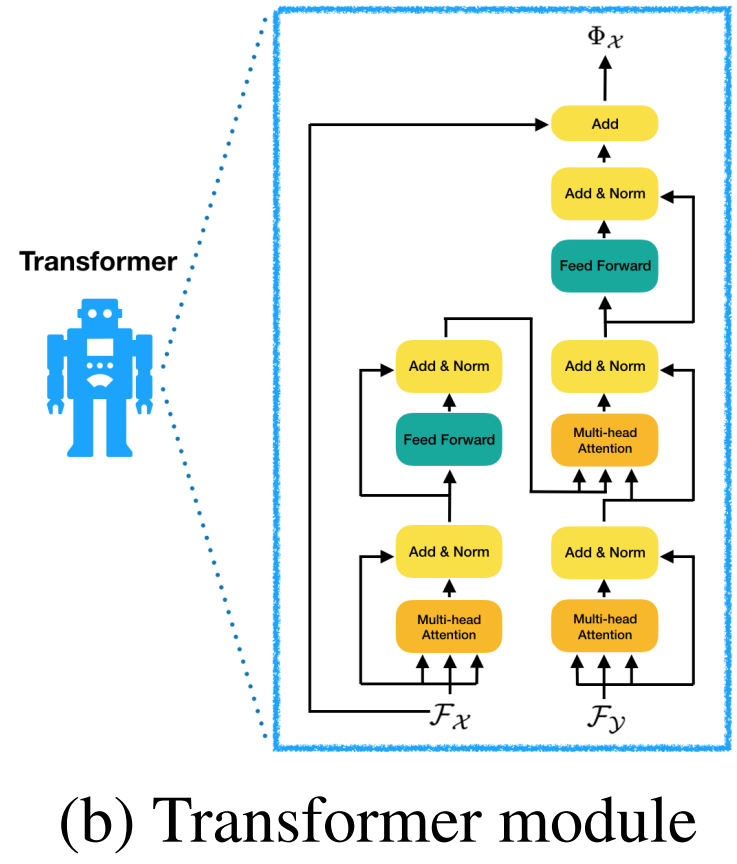
2.3 匹配过程
相对于传统的寻找匹配点对的方式(这一过程不可导),本文采用的是 soft map 方式,可以理解 x 一个点不是和 Y 中某一个的点匹配,而是由 Y 生成一个 x 匹配的目标点的位置,与此位置实现关联。这一点可以近似理解为是差值,这一差值是由 Y 中所有点加权平均得到,我们所学习的 “匹配” 就是求这样的权重向量(soft map)。对于每一个点 \(\boldsymbol{x}_{i}\in\mathcal{X}\),其相对于点集 \(\mathcal{Y}\) 的 soft map 公式如下:
\(m\left(\boldsymbol{x}_{i}, \mathcal{Y}\right)=\operatorname{softmax}\left(\Phi_{\mathcal{Y}} \Phi_{\boldsymbol{x}_{i}}^{\top}\right) \tag{2}\)其中 \(\Phi_{\mathcal{Y}}\in\mathbb{R}^{N\times P}\) 表示由 \(\mathcal{Y}\) 生成的 Embeding,\(\Phi_{\boldsymbol{x}_{i}}\) 代表 \(\Phi_{\boldsymbol{x}}\) 的第 i 行。
2.4 SVD模块
与《Least-Squares Rigid Motion Using SVD》文章相同,本文最终也是使用 SVD 求解 R、t,匹配的点是使用上述 soft map 重新生成的点云,生成函数如下:
\(\hat{\boldsymbol{y}}_{i}=Y^{\top} m\left(\boldsymbol{x}_{i}, \mathcal{Y}\right) \in \mathbb{R}^{3} \tag{3}\)这里定义 \(Y\in\mathbb{R}^{N\times 3}\) 是 \(\mathcal{Y}\) 所有点坐标排列组成的矩阵。这样转换为新的匹配点对 \(\boldsymbol{x}_{i}\mapsto\hat{\boldsymbol{y}}_{i}\) 最终就可以用 SVD 方法求解 R 、t了。
2.5 Loss
误差函数设计比较简单,因为是回归 Pose,所以采用的是典型的 R 和 t 回归的方式:
\(\mathrm{Loss}=\left\|\boldsymbol{R}_{\mathcal{X} \mathcal{Y}}^{\top} \boldsymbol{R}_{\mathcal{X} \mathcal{Y}}^{g}-I\right\|^{2}+\left\|\boldsymbol{t}_{\mathcal{X} \mathcal{Y}}-\boldsymbol{t}_{\mathcal{X} \mathcal{Y}}^{g}\right\|^{2}+\lambda\|\theta\|^{2} \tag{4}\)其中 g 代表真值(Ground Truth),\(\theta\) 是正则项。
PS:感觉误差函数没有精心设计,一个是 R 没有采用李代数,一个是 R 和 t 没有分别赋予权重,不知道是因为效果足够还是在这里并没有必要。
3 实验
实验部分作者做得还是比较详细的,比如比较 PointNet 和 DGCNN 效果,MLP 与 SVD 求解姿态效果,都能够证明本文方法的有效性。这里简单做一些摘要,详细的实验方法和数据建议阅读原文。
作者将是否使用 Attention 机制的 DCP 算法分别称作 DCPv1 和 DCPv2,下面的实验数据中均有所体现。
3.1 迁移能力 & 鲁棒性
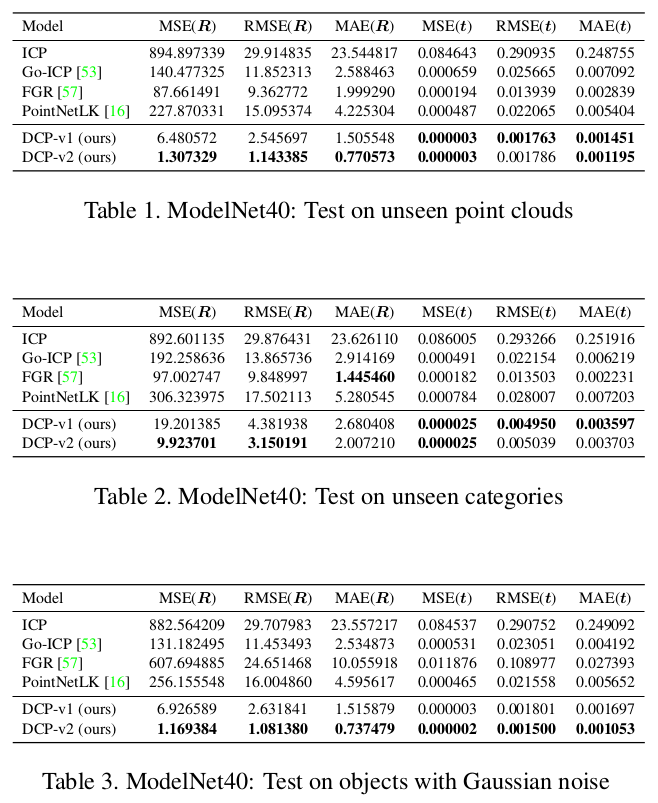
为了证明算法迁移能力作者在 ModelNet40 数据集上做了以下3组实验:
1)在一部分测试集中进行训练一部分未见过的数据集中进行测试(Table 1)
2)在一部分分类中进行训练在另一部分分类中进行测试(Table 2)
3)在测试数据中加入高斯噪声(Table 3)
实验效果均表明 DCP 可以取得很好的效果。
3.2 DCP 后使用 ICP 精调
如下图所示,在一些 Model 上虽然 DCP 可以给出非常接近于真值的 Pose,但是如果再加入 ICP 在此基础上精调的话取得的效果几乎等同于真值(我觉得这里最好是用基于优化的 ICP)。

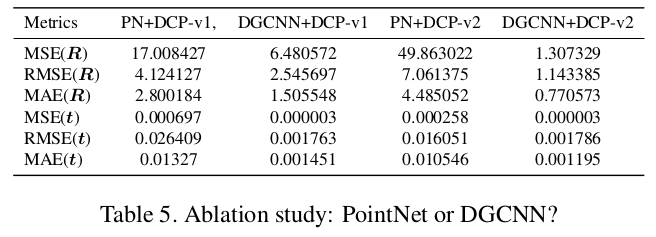
3.3 PointNet 与 DGCNN 对比
在特征提取部分作者推荐他自己的 DGCNN,并与广为使用的 PointNet 做了对比试验,结果表明 DGCNN 具有明显的优势。
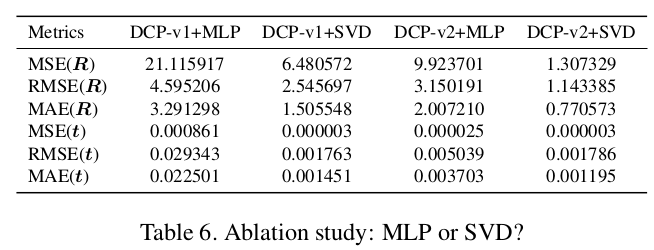
3.4 SVD 与 MLP 对比
很多基于 Deep Learning 方法的 Pose 回归直接使用 MLP,其实这样很不科学,但是似乎也很 work。作者也对 MLP 和 SVD 方法进行了对比,结果表明更加科学的 SVD 明显具有更好的精度(所以不要搞什么 MLP 回归 Pose 的东西了)。
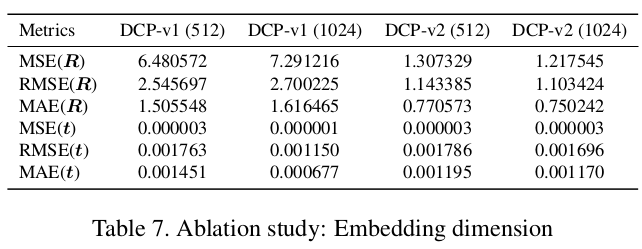
3.5 Embedding 维度
对于 Embedding 维度作者也进行了对比,结果表明对于 DCPv1 维度从 512 提升到 1024 效果有更明显提升,但是 DCPv2 提升不明显。
个人小结
这篇文章从 SVD 求解 ICP 问题的细节原理出发,针对 ICP 问题定制了网络模型,分析非常细致而且也做了比较充足的实验,比如比较 PointNet 和 DGCNN 效果,MLP 与 SVD 求解姿态效果,都能够证明本文方法的有效性。
在我们的复现过程中,实际上重新生成的点云形状看起来和目标点云很不像,然而最终结果至少在 3D 上还是不错的,这一点 Transformer 起到的作用是不是和文章中所述还是比较迷。
相关材料
原文PDF:
