论文笔记:GCNv2: Efficient Correspondence Prediction for Real-Time SLAM
GCNv2 是一个专门针对几何匹配的描述子网络,是对 GCN 的改进版主要工作如下:1)与常见深度学习特征匹配的性能并且显著减少了前向运算的时间;2)加入了二值化层,生成二值特征。
1 GCNv2 网络结构
GCNv2 网络结构如下图所示:
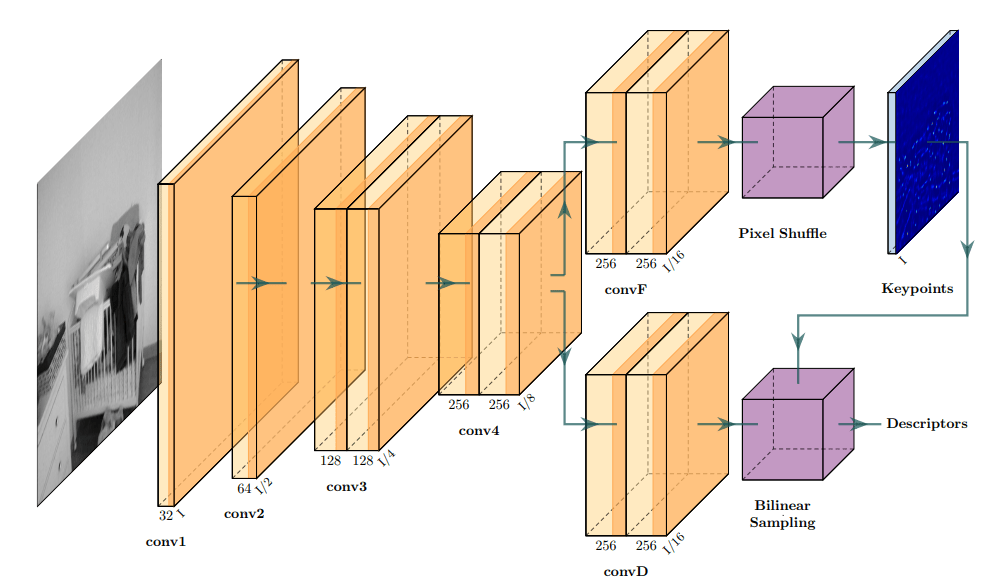
这一结构不必赘述,其实跟 SuperPoint 很像,不过 Descriptors 部分是把 Keypoints 直接拿来取了相应的部分。PixelShuffle (有人也叫作 Sub-pixel Convolution 或者亚像素卷积)在文章(《Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network》)中讲过,它的大概思想如下图所示:
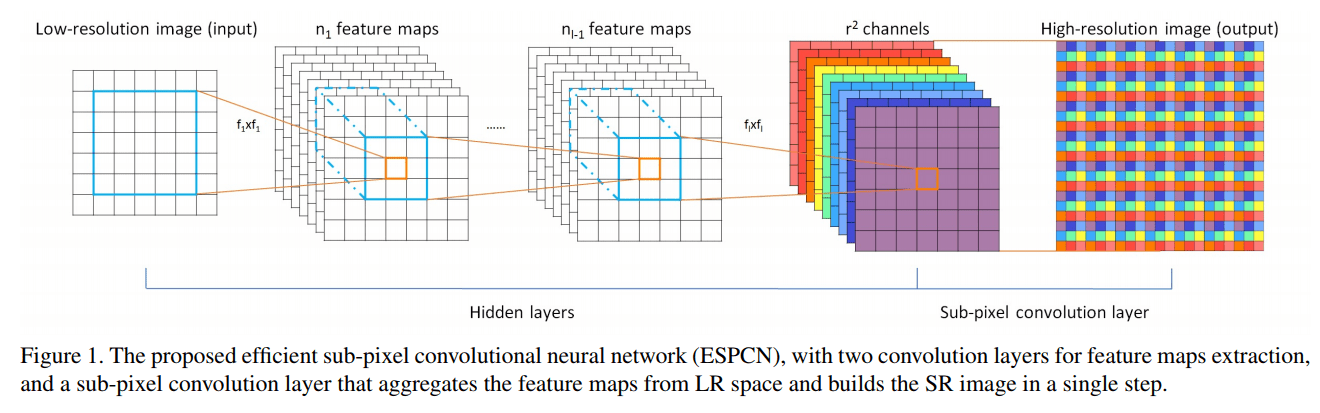
它的效果是将一个 \(H \times W\) 的低分辨率输入图像(Low Resolution),通过Sub-pixel操作将其变为 \(rH\times rW\) 的高分辨率图像(High Resolution)。
但是其实现过程不是直接通过插值等方式产生这个高分辨率图像,而是通过卷积先得到 个通道的特征图(特征图大小和输入低分辨率图像一致),然后通过周期筛选(periodic shuffing)的方法得到这个高分辨率的图像,其中 \(r\) 为上采样因子(upscaling factor),也就是图像的扩大倍率。
图中双层的表示连续两个卷积。具体可以看他的实现代码其实非常明晰:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
class GCNv2(torch.nn.Module): def __init__(self): super(GCNv2, self).__init__() self.elu = torch.nn.ELU(inplace=True) self.conv1 = torch.nn.Conv2d(1, 32, kernel_size=4, stride=2, padding=1) self.conv2 = torch.nn.Conv2d(32, 64, kernel_size=4, stride=2, padding=1) self.conv3_1 = torch.nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1) self.conv3_2 = torch.nn.Conv2d(128, 128, kernel_size=4, stride=2, padding=1) self.conv4_1 = torch.nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1) self.conv4_2 = torch.nn.Conv2d(256, 256, kernel_size=4, stride=2, padding=1) # Descriptor self.convF_1 = torch.nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1) self.convF_2 = torch.nn.Conv2d(256, 256, kernel_size=1, stride=1, padding=0) # Detector self.convD_1 = torch.nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1) self.convD_2 = torch.nn.Conv2d(256, 256, kernel_size=1, stride=1, padding=0) self.pixel_shuffle = torch.nn.PixelShuffle(16) def forward(self, x): x = self.elu(self.conv1(x)) x = self.elu(self.conv2(x)) x = self.elu(self.conv3_1(x)) x = self.elu(self.conv3_2(x)) x = self.elu(self.conv4_1(x)) x = self.elu(self.conv4_2(x)) # Descriptor xF xF = self.elu(self.convF_1(x)) desc = self.convF_2(xF) dn = torch.norm(desc, p=2, dim=1) # Compute the norm. desc = desc.div(torch.unsqueeze(dn, 1)) # Divide by norm to normalize. # Detector xD xD = self.elu(self.convD_1(x)) det = self.convD_2(xD).sigmoid() det = self.pixel_shuffle(det) return desc, det |
为了在移动端上更快,作者还提出了 GCNv2-tiny,进一步压缩了参数(主要是把 conv2 和之后的卷积通道数减半),达到了 TX2 上实时(40Hz)的效果。GCNv2-tiny 的代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
class GCNv2_tiny(torch.nn.Module): def __init__(self): super(GCNv2_tiny, self).__init__() self.elu = torch.nn.ELU(inplace=True) self.conv1 = torch.nn.Conv2d(1, 32, kernel_size=4, stride=2, padding=1) self.conv2 = torch.nn.Conv2d(32, 32, kernel_size=4, stride=2, padding=1) self.conv3_1 = torch.nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1) self.conv3_2 = torch.nn.Conv2d(64, 64, kernel_size=4, stride=2, padding=1) self.conv4_1 = torch.nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1) self.conv4_2 = torch.nn.Conv2d(128, 128, kernel_size=4, stride=2, padding=1) # Descriptor self.convF_1 = torch.nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1) self.convF_2 = torch.nn.Conv2d(256, 256, kernel_size=1, stride=1, padding=0) self.convD_1 = torch.nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1) self.convD_2 = torch.nn.Conv2d(256, 256, kernel_size=1, stride=1, padding=0) self.pixel_shuffle = torch.nn.PixelShuffle(16) def forward(self, x): x = self.elu(self.conv1(x)) x = self.elu(self.conv2(x)) x = self.elu(self.conv3_1(x)) x = self.elu(self.conv3_2(x)) x = self.elu(self.conv4_1(x)) x = self.elu(self.conv4_2(x)) # Descriptor xF xF = self.elu(self.convF_1(x)) desc = self.convF_2(xF) dn = torch.norm(desc, p=2, dim=1) # Compute the norm. desc = desc.div(torch.unsqueeze(dn, 1)) # Divide by norm to normalize. # Detector xD xD = self.elu(self.convD_1(x)) det = self.convD_2(xD).sigmoid() det = self.pixel_shuffle(det) return desc, det |
2 特征提取
2.1 定义
我们令 \(f\) 表示 convD 中提取的压缩尺度的特征图,\(o\) 表示 PixelShuffle 提取的原始大小的关键点热点图。当我们给出一个图像坐标系的坐标 \(x = (u, v)\),显然我们能够得到其在 \(f\left( \cdot \right)\) 和 \(\\o\left( \cdot \right)\) 的对应位置坐标,需要注意的是,由于 \(f\) 是缩略尺寸特征,其描述是通过双线性插值得到的。上角标表示输入的是 current 还是 target 帧(例如:\(f^{cur}\) 或 \(f^{tar}\))。另外,\(L_{feat}\) 表示 descriptor 的损失函数,\(L_{det}\) 表示 detector 的损失函数。
2.2 二值特征
为了获取描述子的二值特征,我们定义了一个 Binary activation layer,它的定义如下(其实只是一个符号函数):
Forward: \(\boldsymbol{b}(\boldsymbol{x})=\operatorname{sign}(\boldsymbol{f}(\boldsymbol{x}))=\left\{\begin{array}{ll}{+1} & {\boldsymbol{f}(\boldsymbol{x}) \geq 0} \\ {-1} & {\text { otherwise }}\end{array}\right.\)
Backward: \( \frac{\partial b}{\partial f}=\mathbf{1}_{|f| \leq 1}\)
作者发现加入这样一个 Binary activation layer 比直接让网络输出 -1~+1 之间的数值效果更好。
这一二值网络来自于论文《Binarized neural networks: Training neural networks with weights and activations constrained to+ 1 or-1》,对其思想简述如下:
2.2.1 预测过程
前向运算
假设 \(W^{k}\) 是第 k 层的权重矩阵,\(x^{k}\) 是第 k 层的输入,则 Binary Layer 的计算过程如下:
\(x^{k}=\sigma\left(W^{k} \cdot x^{k-1}\right)\)其中 \(\sigma( \cdot )\) 是二值化的激活函数其定义如下:
\(\sigma(x)=\operatorname{sign}(x)=\left\{\begin{array}{ll}{+1} & {\text { if } x \geq 0} \\ {-1} & {\text { otherwise }}\end{array}\right.\)2.2.2 训练过程
由于网络参数已经二值化,直接正向或者负向调整会导致模型震荡 ,因此不能直接进行更新,为了解决这个问题,权值和梯度在训练过程中保持全精度。
前馈运算(神经网络后一层向前一层的传播)
作者给出了一个例子,以BN层的二值化为例,先将实数型权值参数二值化得到二值型权值参数,即 \(W_{k}^{b}=\operatorname{sign}\left(W_{k}\right)\)。然后利用二值化后的参数计算得到实数型的中间向量,该向量再通过 \(BN(⋅)\) 即 Batch Normalization 操作,得到实数型的隐藏层激活向量。如果不是输出层的话,就将该向量二值化。
\(x^{k}=\sigma\left(B N\left(W_{b}^{k} \cdot x^{k-1}\right)=\operatorname{sign}\left(B N\left(W_{b}^{k} \cdot x^{k-1}\right)\right)\right.\)反向传播
由于 \(σ(⋅)\) 基本上是一个梯度处处为零的函数,其不适合用于反向传播,因此 Binarized neural networks 提出采用借鉴 Yoshua Benjio 在 2013年 的时候通过 “straight-through estimator” 随机离散化神经元来进行梯度计算和反向传播的工作。也就是将 \(σ(x)=sign(x)\) 近似为下面的函数:
\(\operatorname{Htanh}(x)=\operatorname{Clip}(x,-1,1)=\max (-1, \min (1, x))\)本质上就是在 -1 与 +1 之间加上一个线性变换过程,导数为1,这样就变成了可导。
如图所示:
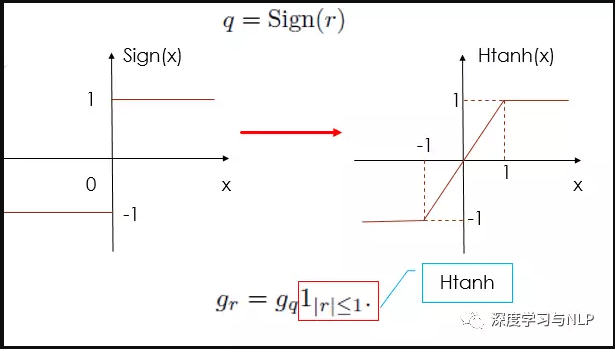
那么解决了 \(Binarize()\) 函数的可导问题之后,后面的就是关于 BN 层二值化的前向和反向传播过程:

2.3 描述子学习
误差函数
二值特征学习部分采用 triplet loss ,其定义如下:
\(L_{f e a t}=\sum_{i} \max \left(0, d\left(\boldsymbol{x}_{i}^{c u r}, \boldsymbol{x}_{i,+}^{\operatorname{tar}}\right)-d\left(\boldsymbol{x}_{i}^{c u r}, \boldsymbol{x}_{i,-}^{\operatorname{tar}}\right)+m\right)\)其中 \(x^{cur}\)表示 anchor, 表示 \(x^{tar}_+\) positive,\(x^{tar}_-\) 表示 negative。距离函数 d 是汉明距离。其公式如下:
\(d\left(\boldsymbol{x}^{c u r}, \boldsymbol{x}^{t a r}\right)=\left\|\boldsymbol{b}^{c u r}\left(\boldsymbol{x}^{c u r}\right)-\boldsymbol{b}^{t a r}\left(\boldsymbol{x}^{t a r}\right)\right\|_{2}\)样本生成
为了找到 target 的正样本,我们采用的是用 Pose 真值获取的方式,也就是将 current 帧的 feature 投影到 target 帧,然后通过寻找最近临的方式获得正样本,投影方式如下:
\(\boldsymbol{x}_{i,+}^{t a r}=\boldsymbol{\pi}^{-1}\left(\mathbf{R}_{g t} \boldsymbol{\pi}\left(\boldsymbol{x}_{i}^{c u r}, z_{i}\right)+\boldsymbol{t}_{g t}\right)\)负样本生成(Exhaustive Negative Sample Mining)如下,该函数会根据阈值 c 返回负样本,也就是大于某个距离的认为是负样本(由于 k nearest 排序,返回的可以认为是最接近正样本的负样本):

其中的 \(b\) 表示量化成二值特征(256bit)的向量。
2.4 检测子学习
2.4.1 误差函数
GCN 没有像其他一些 local feature 网络一样学习一张热力图之类,而是直接生成了一张表示是否为关键点的二值图(0 表示不是关键点,1 表示是关键点),那么整个检测子就变成了一个分类问题。所以使用的就是分类问题的 Cross-entropy loss,由于正负样本数不均衡,所以使用 weighted cross-entropy loss。检测子 loss 如下:
\(L_{d e t}=L_{c e}\left(\boldsymbol{o}^{c u r}\left(\boldsymbol{x}^{c u r}\right)\right)+L_{c e}\left(\boldsymbol{o}^{tar}\left(\boldsymbol{x}_{+}^{tar}\right)\right)\)其中 \(l_{ce}\) 就是 weighted cross-entropy loss 定义如下,其中 \(\alpha_1\) 和 \(\alpha_2\) 是正负样本权重系数:
\(\begin{aligned} L_{c e}(\boldsymbol{o}(\boldsymbol{x}))=&-\alpha_{1} \sum_{i} c_{\boldsymbol{x}_{i}} \log \left(\boldsymbol{o}\left(\boldsymbol{x}_{i}\right)\right) \\ &-\alpha_{2} \sum_{i}\left(1-c_{x_{i}}\right) \log \left(1-\boldsymbol{o}\left(\boldsymbol{x}_{i}\right)\right) \end{aligned}\)2.4.2 样本生成
文章中使用 Shi-Tomasi corners (16x16)生成检测子,并对不同帧进行了 warp 操作获得另一帧上检测子位置。为什么不用每帧检测 Shi-Tomasi corners 而用投影方式呢?作者的解释是:This leads to better distribution of keypoints and the objective function directly reflects the ability to track the keypoints based on texture. 也就是说这样生成样本能够反映关键点的跟踪能力。也就是在不同帧关键点位置的鲁棒性。但另一方面,我没有特别明白的是,如果 warp 过去的位置,实际上被遮挡或者什么原因并不能匹配,这种方式会不会选择了错误的匹配对呢?
3 训练细节
总的 Loss 是 \(L_{feat}\) 和 \(L_{det}\) 的和,不过赋予了不同权重。在 GCNv2 中分别赋予权重 100 和 1。其他上述公式中提到的一些参数如下:
| 参数 | 赋值 |
|---|---|
|
\(m\)
|
1 |
|
\(\alpha_1\)
|
0.1 |
|
\(\alpha_2\)
|
1.0 |
| Adam |
初始值 \(10^{-4}\),每40 epoch 下降一半 |
4 实验结果
4.1 整体流程
GCNv2 整体流程如下图所示,其实就是整个代替了 ORB 的检测、描述与匹配过程。
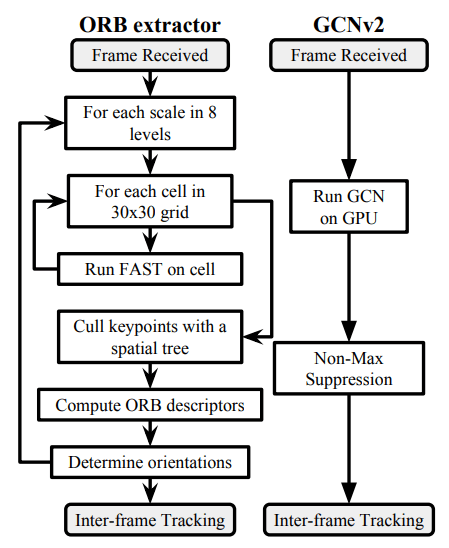
在实验结果方面,GCNv2 取得了比 ORB-SLAM2 更高的精度,同时在 GPU 可以保持实时性能。
4.2 VO 跟踪结果
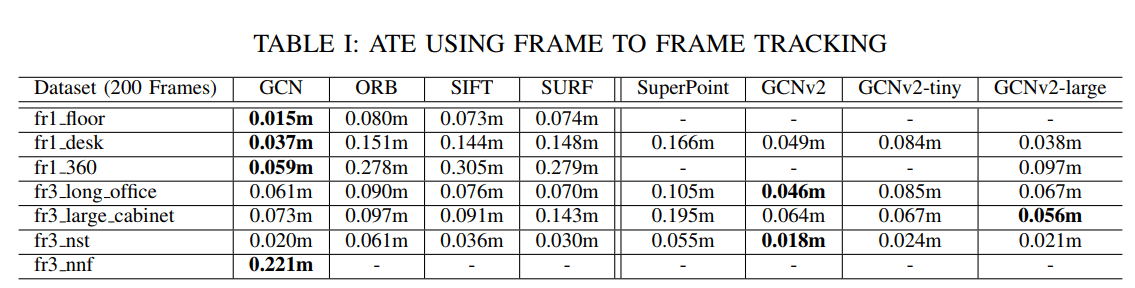
作者做了比较详细的比较,可以看到基本上精度秒杀 ORB ,即使和 SIFT 之类比也不逊色。比较有意思的是 SuperPoint 这种同样是学习的特征,其实换到 ORB SLAM 里面并没有明显优势,甚至很多数据集上还不如 ORB。这和我们之前实验的结果也比较相近。不过这里面有很多 trick,比如特征匹配时间影响 Local Mapping 优化速度,亚像素精度等等都是有影响的,并不能简单从这里说明描述子好效果就一定好。
4.3 加入闭环 SLAM 结果
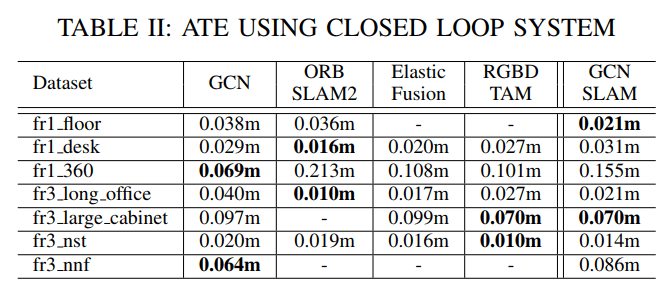
可以看出加入闭环后,ORB SLAM2 效果还是不错的并没有 VO 那么明显,在部分测试集中表现甚至高于 GCN SLAM。不过整体而言 ORB SLAM2 有两个失败,而 GCN SLAM 表现稳定,显示出在鲁棒性方面还是有一定的优势。
4.4 匹配效率
作者比较了 GCNv2-tiny 和 ORB 的匹配效率:
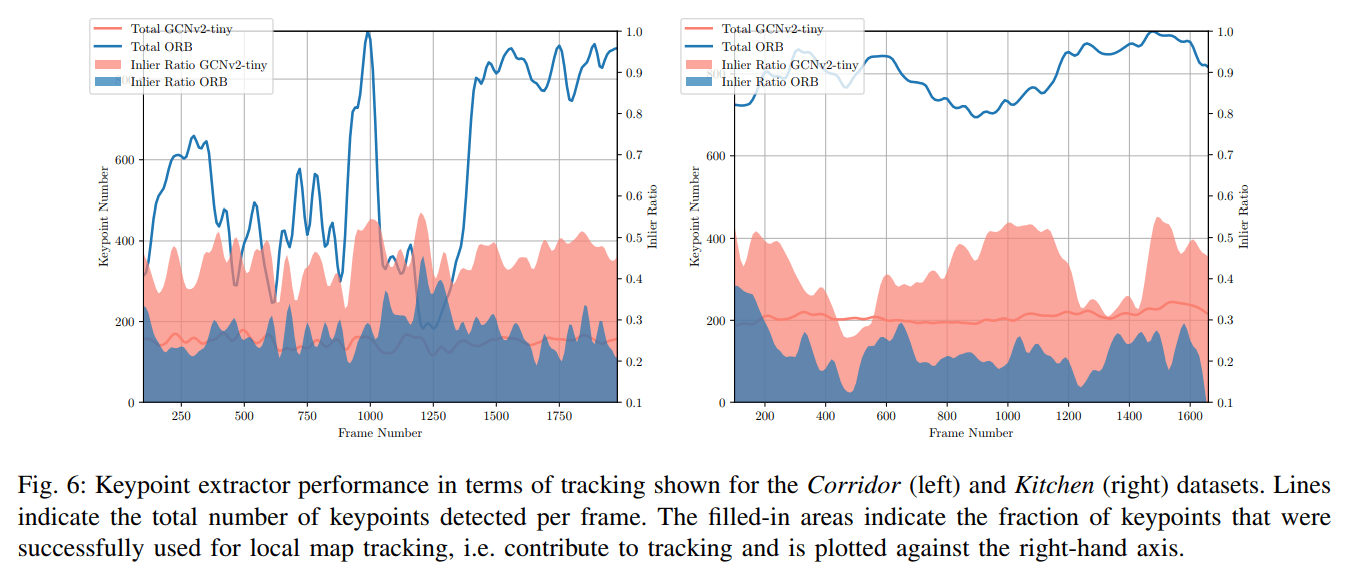
可以看到 GCNv2-tiny 提取点个数更少而内点个数更多,表明其匹配效率较高。
点评
使用 Deep Learning 方式,但是实际上学习的是传统的检测子,感觉没有 MagicPoint 和 SuperPoint 定义更加贴近 ”语义特征点“。不过相对来说生成数据非常容易,仅依赖于 Pose 真值(往往是把 Vicon 或者激光这种当做真值)。可以理解为学习这些描述子是为了 ”fit“ pose(迁移性能有待验证,比如有些描述子遮挡了根本就不能匹配)。整体效果也还不错,而且二值描述子在存储空间和速度上有优势。
参考文献
- Binarized neural networks: Training neural networks with weights and activations constrained to+ 1 or-1笔记:https://zhuanlan.zhihu.com/p/24679842
- Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network 笔记:https://blog.csdn.net/g11d111/article/details/82855946
- https://zhuanlan.zhihu.com/p/26600748
- https://zhuanlan.zhihu.com/p/60049140

你好 请问你可以分享一下GCNv2中计算特征点和描述子以及网络损失这块的代码吗?
你好,因为实测效果并没有 SuperPoint 系列稳定,我目前还没有尝试复现过它的训练过程。
作者的代码都在:https://github.com/jiexiong2016/GCNv2_SLAM
你好,请教下,论文中网络最终输出的结果应该是一个包含特征点的[320,240]的heatmpa图和一个对应描述子的[256,320,240]的featuremap才对。但是我看源码中,对于模型输出的两个tensor,得到的值pst=[num_points, 3]和desc=[num_points,32]。请问下这里对应的是做了哪些操作么?