论文笔记：Dynamic Graph CNN for Learning on Point Clouds

2019年7月31日

Table of Contents

DGCNN 是对 PointNet 的改进，PointNet 网络每个点单独提取特征缺乏局部关联。DGCNN 提出了 EdgeConv 就是对它的改进。

1 网络结构

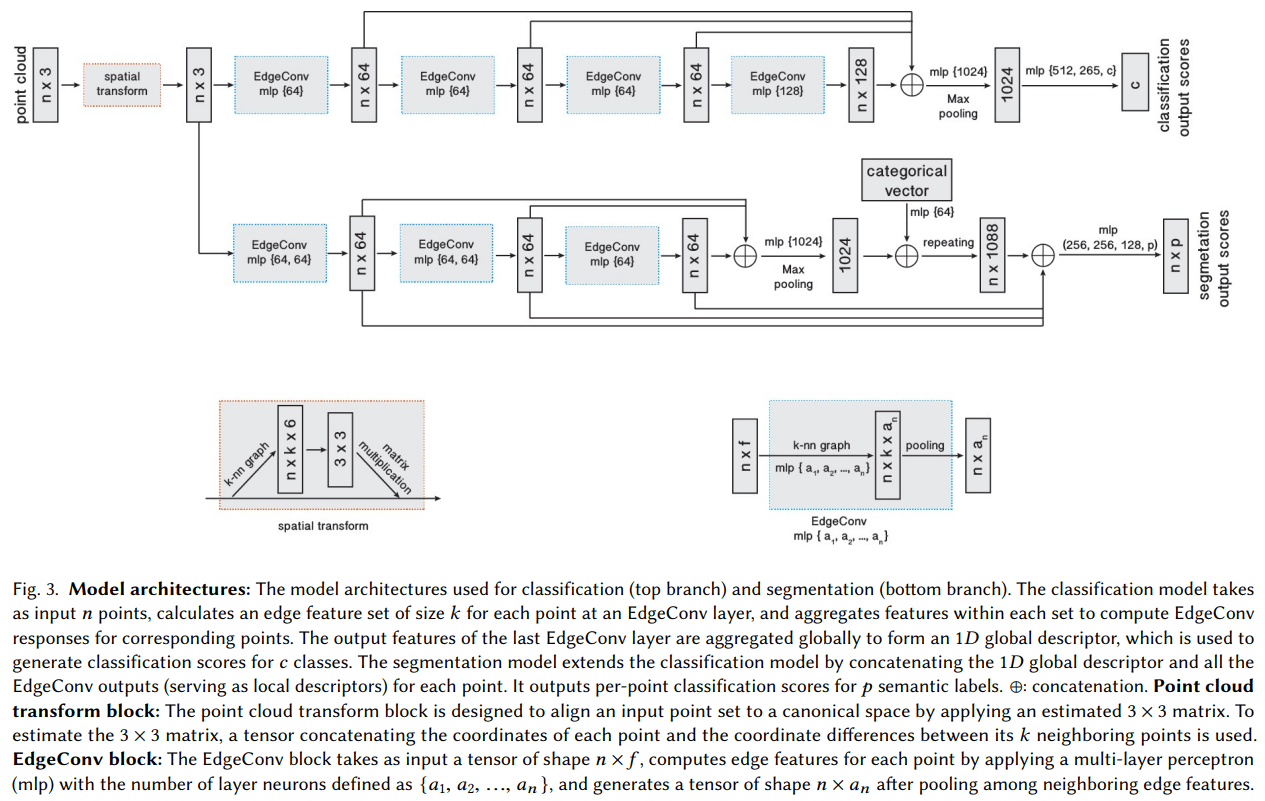
DGCNN 网络结构如下图所示，可以看出其整体架构和 PointNet 是基本一致的，主要区别就是将其中的 MLP 替换成了 EdgeConv。

2 EdgeConv

2.1 EdgeConv 结构

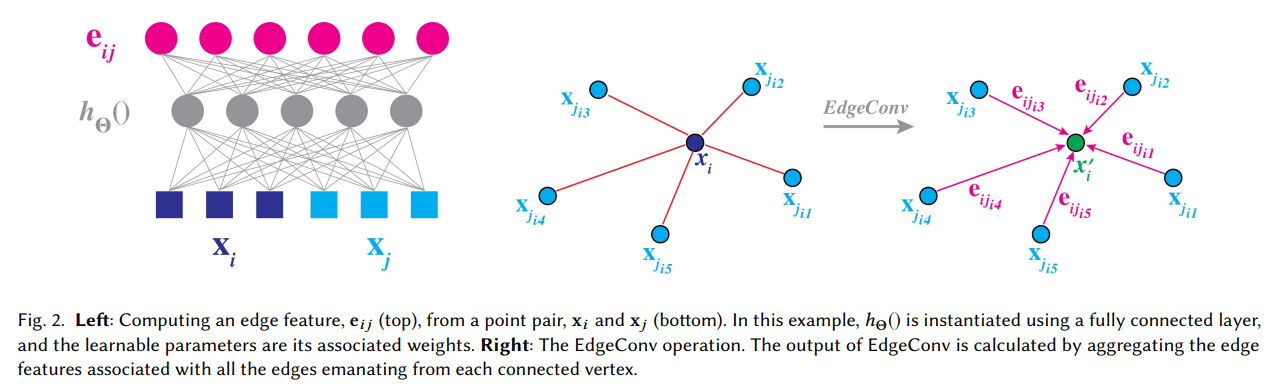
上图是 EdgeConv 的示意图。假设一个F维点云 $\mathbf{X}=\left\{\mathbf{x}_{1}, \dots, \mathbf{x}_{n}\right\} \subseteq \mathbb{R}^{F}$ 其中 F 表示每个点的维度，最简单的可能是 x, y, z 三维，另外还可能引入每个点颜色、法线等信息。给定一个有向图 $\mathcal{G}=(\mathcal{V}, \mathcal{E})$ 用来表示点云的局部结构，其中顶点为 $\mathcal{V}=\{1, \ldots, n\}$ ，边为 $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$ 。在一个简单例子中，我们用 $\mathcal{G}$ 表示 k-nearest neighbor (k-NN) 图。针对上图有如下定义：

点和边缘：定义 $x_i$ 周围最近 k 个点 $x_{j_{i 1}}, \ldots, x_{j_{i k}}$ ，其有向边为 $\left(i, j_{i 1}\right), \ldots,\left(i, j_{i k}\right)$
边缘特征函数：定义边缘特征为 $e_{i j}=h_{\Theta}\left(x_{i}, x_{j}\right)$ ，其中 $h_{\Theta} : \mathbb{R}^{F} \times \mathbb{R}^{F} \rightarrow \mathbb{R}^{F^{\prime}}$ 是一些使用一些可学习的参数 $\Theta$ 构成的非线性函数。
特征聚合函数：对于边缘特征进行聚合的函数定义为□，其定义是：

\begin{aligned}\mathbf{x}_{i}^{\prime}=\square_{j :(i, j) \in \mathcal{E}} h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\end{aligned}\tag{1}

上述KNN图中的K值是一个超参，分类网络中K=20，而在分割网络中K=30。

关于公式中的 $h$ 和 □ 有四种可能的选择：

第一种：认为 $x_i$ 的特征是周围所有点的加权求和，这一点类似于图像的卷积操作，其中每个卷积核为 $\theta_{m}$ ， $\Theta=\left(\theta_{1}, \ldots, \theta_{M}\right)$ 表示所有卷积核的集合。其公式如下：

$\begin{aligned}x_{i m}^{\prime}=\sum_{j :(i, j) \in \mathcal{E}} \boldsymbol{\theta}_{m} \cdot \mathbf{x}_{j}\end{aligned}\tag{2}$
第二种：描述了一种仅考虑全局特征的形式，即只有关注点 $x_i$ 。其公式如下：

$\begin{aligned}h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=h_{\Theta}\left(\mathbf{x}_{i}\right)\end{aligned}\tag{3}$
第三种：只关注周围特征形式。其公式如下：

$\begin{aligned}h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=h_{\Theta}\left(\mathbf{x}_{j}\right)\end{aligned}\tag{4}$
其中：

$\begin{aligned}x_{i m}^{\prime}=\sum_{j \in \mathcal{V}}\left(h_{\boldsymbol{\theta}\left(\mathbf{x}_{j}\right)}\right) g\left(u\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\right)\end{aligned}\tag{5}$
其中 $g$ 表示高斯核， $u$ 表示两个点的欧氏距离。当然在输入层是坐标之间的欧氏距离，后面的层级中，这个函数表示的是两个点特征向量的欧氏距离。

第四种：只关注局部特征形式，输入仅为点和周围点的差。其公式如下：

$\begin{aligned}h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=h_{\Theta}\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)\end{aligned}\tag{6}$
第五种：同时关注全局特征和局部特征，这也是本文中的主要形式：

$\begin{aligned}h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\overline{h}_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}-\mathbf{x}_{i}\right)\end{aligned}\tag{7}$
在本文中我们使用：

$\begin{aligned}e_{i j m}^{\prime}=\operatorname{ReLU}\left(\boldsymbol{\theta}_{m} \cdot\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)+\boldsymbol{\phi}_{m} \cdot \mathbf{x}_{i}\right)\end{aligned}\tag{8}$
该项可以用 shared MLP 表示，最后使用 max 进行特征聚合：

$\begin{aligned}x_{i m}^{\prime}=\max _{j :(i, j) \in \mathcal{E}} e_{i j m}^{\prime}\end{aligned}\tag{9}$
全部超参数集合为： $\Theta=\left(\theta_{1}, \ldots, \theta_{M}, \phi_{1}, \ldots, \phi_{M}\right)$

4.2 EdgeConv 实现

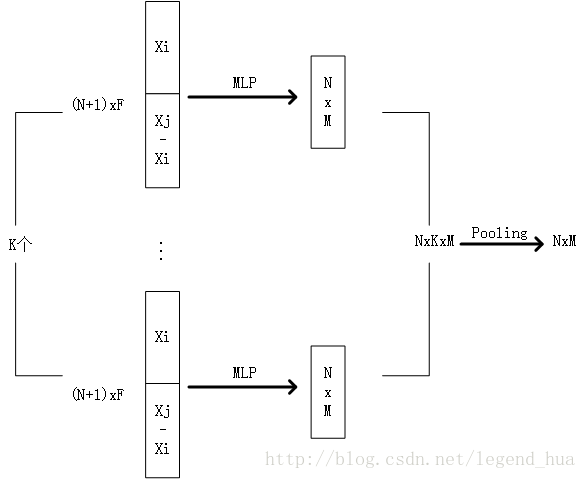
输入为NxF的张量，其中包括原数据Xi和与其附近的K个点。首先原数据的每个点和附件的K个点，通过MLP生成K个NxM特征，即NxKxM，最后通过一个pooling操作输出NxM特征。

看它的代码更清晰：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@Author: Yue Wang
@Contact: yuewangx@mit.edu
@File: model.py
@Time: 2018/10/13 6:35 PM
"""


import os
import sys
import copy
import math
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F


def knn(x, k):
    inner = -2*torch.matmul(x.transpose(2, 1), x)
    xx = torch.sum(x**2, dim=1, keepdim=True)
    pairwise_distance = -xx - inner - xx.transpose(2, 1)
 
    idx = pairwise_distance.topk(k=k, dim=-1)[1]   # (batch_size, num_points, k)
    return idx


def get_graph_feature(x, k=20, idx=None):
    batch_size = x.size(0)
    num_points = x.size(2)
    x = x.view(batch_size, -1, num_points)
    if idx is None:
        idx = knn(x, k=k)   # (batch_size, num_points, k)
    device = torch.device('cuda')

    idx_base = torch.arange(0, batch_size, device=device).view(-1, 1, 1)*num_points

    idx = idx + idx_base

    idx = idx.view(-1)
 
    _, num_dims, _ = x.size()

    x = x.transpose(2, 1).contiguous()   # (batch_size, num_points, num_dims)  -> (batch_size*num_points, num_dims) #   batch_size * num_points * k + range(0, batch_size*num_points)
    feature = x.view(batch_size*num_points, -1)[idx, :]
    feature = feature.view(batch_size, num_points, k, num_dims) 
    x = x.view(batch_size, num_points, 1, num_dims).repeat(1, 1, k, 1)
    
    feature = torch.cat((feature-x, x), dim=3).permute(0, 3, 1, 2)
  
    return feature


class DGCNN(nn.Module):
    def __init__(self, args, output_channels=40):
        super(DGCNN, self).__init__()
        self.args = args
        self.k = args.k
        
        self.bn1 = nn.BatchNorm2d(64)
        self.bn2 = nn.BatchNorm2d(64)
        self.bn3 = nn.BatchNorm2d(128)
        self.bn4 = nn.BatchNorm2d(256)
        self.bn5 = nn.BatchNorm1d(args.emb_dims)

        self.conv1 = nn.Sequential(nn.Conv2d(6, 64, kernel_size=1, bias=False),
                                   self.bn1,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv2 = nn.Sequential(nn.Conv2d(64*2, 64, kernel_size=1, bias=False),
                                   self.bn2,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv3 = nn.Sequential(nn.Conv2d(64*2, 128, kernel_size=1, bias=False),
                                   self.bn3,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv4 = nn.Sequential(nn.Conv2d(128*2, 256, kernel_size=1, bias=False),
                                   self.bn4,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv5 = nn.Sequential(nn.Conv1d(512, args.emb_dims, kernel_size=1, bias=False),
                                   self.bn5,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.linear1 = nn.Linear(args.emb_dims*2, 512, bias=False)
        self.bn6 = nn.BatchNorm1d(512)
        self.dp1 = nn.Dropout(p=args.dropout)
        self.linear2 = nn.Linear(512, 256)
        self.bn7 = nn.BatchNorm1d(256)
        self.dp2 = nn.Dropout(p=args.dropout)
        self.linear3 = nn.Linear(256, output_channels)

    def forward(self, x):
        batch_size = x.size(0)
        x = get_graph_feature(x, k=self.k)
        x = self.conv1(x)
        x1 = x.max(dim=-1, keepdim=False)[0]

        x = get_graph_feature(x1, k=self.k)
        x = self.conv2(x)
        x2 = x.max(dim=-1, keepdim=False)[0]

        x = get_graph_feature(x2, k=self.k)
        x = self.conv3(x)
        x3 = x.max(dim=-1, keepdim=False)[0]

        x = get_graph_feature(x3, k=self.k)
        x = self.conv4(x)
        x4 = x.max(dim=-1, keepdim=False)[0]

        x = torch.cat((x1, x2, x3, x4), dim=1)

        x = self.conv5(x)
        x1 = F.adaptive_max_pool1d(x, 1).view(batch_size, -1)
        x2 = F.adaptive_avg_pool1d(x, 1).view(batch_size, -1)
        x = torch.cat((x1, x2), 1)

        x = F.leaky_relu(self.bn6(self.linear1(x)), negative_slope=0.2)
        x = self.dp1(x)
        x = F.leaky_relu(self.bn7(self.linear2(x)), negative_slope=0.2)
        x = self.dp2(x)
        x = self.linear3(x)
        return x

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

#!/usr/bin/env python

# -*- coding: utf-8 -*-

"""

@Author: Yue Wang

@Contact: yuewangx@mit.edu

@File: model.py

@Time: 2018/10/13 6:35 PM

"""

import os

import sys

import copy

import math

import numpy as np

import torch

import torch.nn as nn

import torch.nn.functional as F

def knn(x, k):

inner = -2*torch.matmul(x.transpose(2, 1), x)

xx = torch.sum(x**2, dim=1, keepdim=True)

pairwise_distance = -xx - inner - xx.transpose(2, 1)

idx = pairwise_distance.topk(k=k, dim=-1)[1] # (batch_size, num_points, k)

return idx

def get_graph_feature(x, k=20, idx=None):

batch_size = x.size(0)

num_points = x.size(2)

x = x.view(batch_size, -1, num_points)

if idx is None:

idx = knn(x, k=k) # (batch_size, num_points, k)

device = torch.device('cuda')

idx_base = torch.arange(0, batch_size, device=device).view(-1, 1, 1)*num_points

idx = idx + idx_base

idx = idx.view(-1)

_, num_dims, _ = x.size()

x = x.transpose(2, 1).contiguous() # (batch_size, num_points, num_dims) -> (batch_size*num_points, num_dims) # batch_size * num_points * k + range(0, batch_size*num_points)

feature = x.view(batch_size*num_points, -1)[idx, :]

feature = feature.view(batch_size, num_points, k, num_dims)

x = x.view(batch_size, num_points, 1, num_dims).repeat(1, 1, k, 1)

feature = torch.cat((feature-x, x), dim=3).permute(0, 3, 1, 2)

return feature

class DGCNN(nn.Module):

def __init__(self, args, output_channels=40):

super(DGCNN, self).__init__()

self.args = args

self.k = args.k

self.bn1 = nn.BatchNorm2d(64)

self.bn2 = nn.BatchNorm2d(64)

self.bn3 = nn.BatchNorm2d(128)

self.bn4 = nn.BatchNorm2d(256)

self.bn5 = nn.BatchNorm1d(args.emb_dims)

self.conv1 = nn.Sequential(nn.Conv2d(6, 64, kernel_size=1, bias=False),

self.bn1,