Policy Gradient (策略梯度)
Policy Gradient (策略梯度) 是强化学习中的基础概念之一,在很多工作中都会使用(特别是对于可微化的工作)。本文内容主要来自于台大李宏毅的教学课件。
下载地址:1636956663-PPO (v3)
1 Policy of Actor
1.1 基本概念
强化学习是根据环境观测、自身动作以及反馈来学习网络的一种方式。它通常有以下一些概念:
- Policy 用 \(\pi\) 表示,它是一个深度神经网络,网络的参数为 \(\theta\)
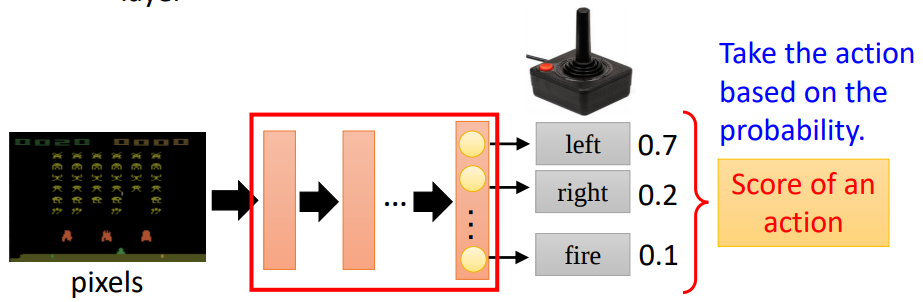
- Actor 用 \(\alpha\) 表示,它是我们可以控制的动作。比如对于上面的游戏例子来说,我们每一步可以选择 left right fire 三种动作。它就是 Policy Gradient 学习的对象
- Environment 表示环境,这是我们无法改变的。我们仅能对其进行观测 Observation
- Reward 用 \(r\) 表示,它是我们采用动作后从环境获得结果。比如对于上面的游戏的例子来说就是当前获得的分数。
- State 用 \(s\) 表示,它是我们当前所处的状态
- Trajectory 用 \(\tau\) 表示 \(a\) 和 \(s\) 的序列。
- Episode 游戏从开始到结束的一个完整回合
对于上面的例子来说,我们所有的 Trajectory 为 \(\tau=\left\{s_{1}, a_{1}, s_{2}, a_{2}, \cdots, s_{T}, a_{T}\right\}\),其概率为(下一步的 State 只和上一步 State 加上 Actor 相关):
\(\begin{array}{l}p_{\theta}(\tau) \\
=p\left(s_{1}\right) p_{\theta}\left(a_{1} \mid s_{1}\right) p\left(s_{2} \mid s_{1}, a_{1}\right) p_{\theta}\left(a_{2} \mid s_{2}\right) p\left(s_{3} \mid s_{2}, a_{2}\right) \cdots \\
=p\left(s_{1}\right) \prod_{t=1}^{T} p_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right)
\end{array}\tag{1}\)
很显然 \(p\left(s_{t+1} \mid s_{t}, a_{t}\right)\) 完全由游戏环境 Environment 决定(又叫环境动力学),我们无法控制;而我们能控制的是 Policy 部分 \(p_{\theta}\left(a_{t} \mid s_{t}\right)\),它与我们的网络参数 \(\theta\) 有关。
1.2 Expected Reward
给定一个 \(\tau\) 我们就能得到一个游戏的完整 Reward:\(R(\tau)=\sum_{t=1}^{T} r_{t}\)。我们学习的目标就是找到最优的 actor 使得 \(R(\tau)\) 最大化。
我们学习的目标就是使得对于所有可能选择的 \(\tau\) 的期望奖励最大:
\(\bar{R}_{\theta}=\sum_{\tau} R(\tau) p_{\theta}(\tau)=E_{\tau \sim p_{\theta}(\tau)}[R(\tau)]\tag{2}\)2 Policy Gradient
2.1 理论推导
为了求解上面的 \(\bar{R}_{\theta}\),我们需要求其梯度 \(\nabla \bar{R}_{\theta}\),推导如下:
\(\begin{aligned}
\nabla \bar{R}_{\theta} &=\sum_{\tau} R(\tau) \nabla p_{\theta}(\tau)=\sum_{\tau} R(\tau) p_{\theta}(\tau) \frac{\nabla p_{\theta}(\tau)}{p_{\theta}(\tau)} \\
&=\sum_{\tau} R(\tau) p_{\theta}(\tau) \nabla \log p_{\theta}(\tau) \\
&=E_{\tau \sim p_{\theta}(\tau)}\left[R(\tau) \nabla \log p_{\theta}(\tau)\right] \approx \frac{1}{N} \sum_{n=1}^{N} R\left(\tau^{n}\right) \nabla \log p_{\theta}\left(\tau^{n}\right) \\
&=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} R\left(\tau^{n}\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)
\end{aligned}\tag{3}\)
对上述推导解释如下:
其中第二个等号用到了如下性质:
\(\nabla f(x)= f(x) \nabla \log f(x)\tag{4}\)
其中约等号的意思是,我们可能不能穷尽所有的 \(\tau\) 来求期望,因此我们可能转而采用一个采样策略获得 N 个采样来得到一个近似的期望估计。
其中最后一个等号的意思是,根据之前的公式(1)有结论:
\(p_{\theta}(\tau) = p\left(s_{1}\right) \prod_{t=1}^{T} p_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right)\tag{5}\)
对于 \(p\left(s_{t+1} \mid s_{t}, a_{t}\right)\) 我们之前已经分析了其是有环境决定的,不能控制也无法求梯度,所以我们只能对 \(p_{\theta}\left(a_{t} \mid s_{t}\right)\) 求梯度,因此得到:
\(\nabla \log p_{\theta}\left(\tau^{n}\right)=\nabla \log \left( p\left(s_{1}\right) \prod_{t=1}^{T_n} p_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right) \right)=\sum_{t=1}^{T_{n}} \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)\tag{6}\)
理解一下最后的 \(\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} R\left(\tau^{n}\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)\):若在 \(s_t^n\) 下执行 \(a_t^n\) 使得 \(R\left(\tau^{n}\right)\) 为正,则增加概率 \(p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)\) ;为负则减少概率。
2.2 实现方法
解决上述优化问题的方法有很多,最常用的为最速下降法,这里称为策略梯度(Policy Gradient)或者策略优化(Policy Optimization)。
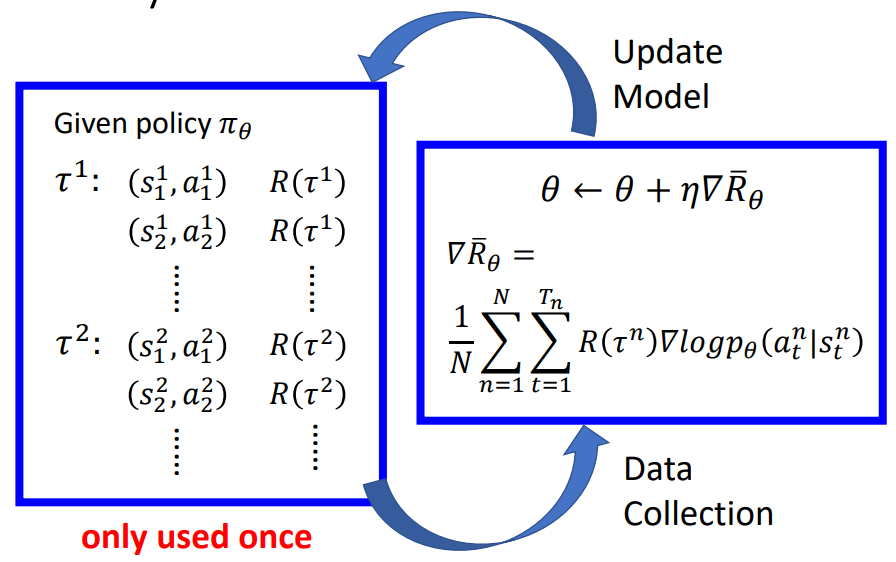
典型的流程如下:
通过左侧方框进行采样若干 sample 作为 data 送入右侧求梯度更新模型,反复迭代。注意这里一次采样的 sample 只能用来进行一次迭代。
2.3 从监督学习角度理解
在监督学习中我们对于分类问题通常使用交叉熵作为损害函数的方式实现,交叉熵定义如下:
其中 \(p(x)\) 为属于哪一类的标签,\(q(x)\) 为网络预测的概率。
\(H(p, q)=-\sum_{x} p(x) \log q(x)\tag{7}\)在 Policy Gradient 里面我们用 Reward 作为我们的 label 定义损失函数,其公式如下:
\(L(\theta)=-\frac{1}{N} \sum_{\tau} R(\tau) \log \pi_{\theta}(\tau)\tag{8}\)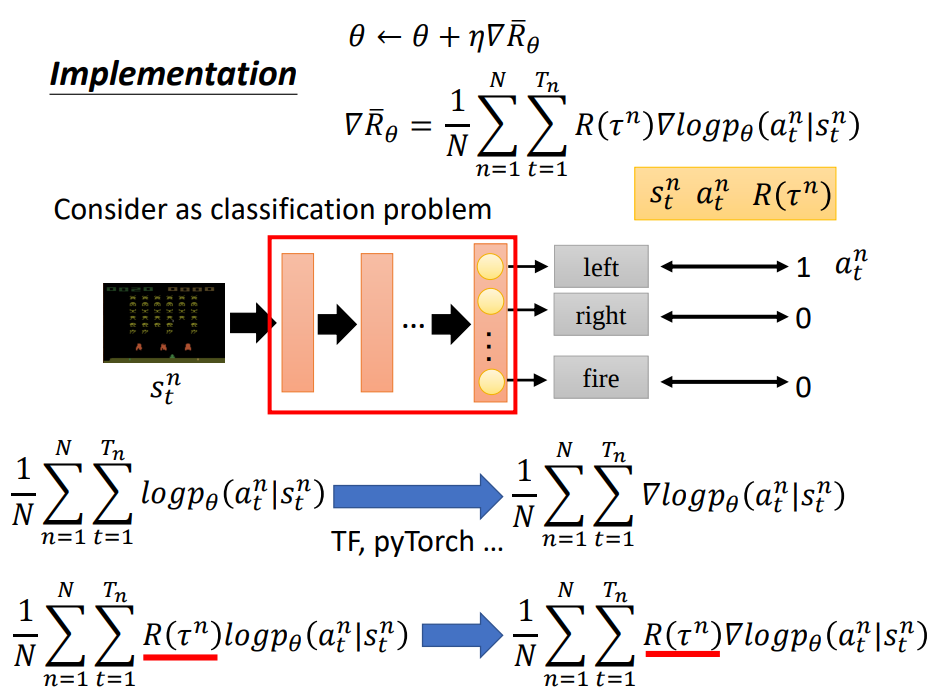
对比上图上面的公式就代表了原来分类问题中交叉熵定义下的损失函数 \(p(x)=1\)
而下面就代表了 Policy Gradient 下用 \(R\) 代替 \(p(x)\) 的损失函数。
参考材料
[1] http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html
[2] https://zhuanlan.zhihu.com/p/107906954
[3] https://blog.csdn.net/cindy_1102/article/details/87905272
[4] https://blog.csdn.net/qq_36829091/article/details/83213707