三角化 | Triangulation

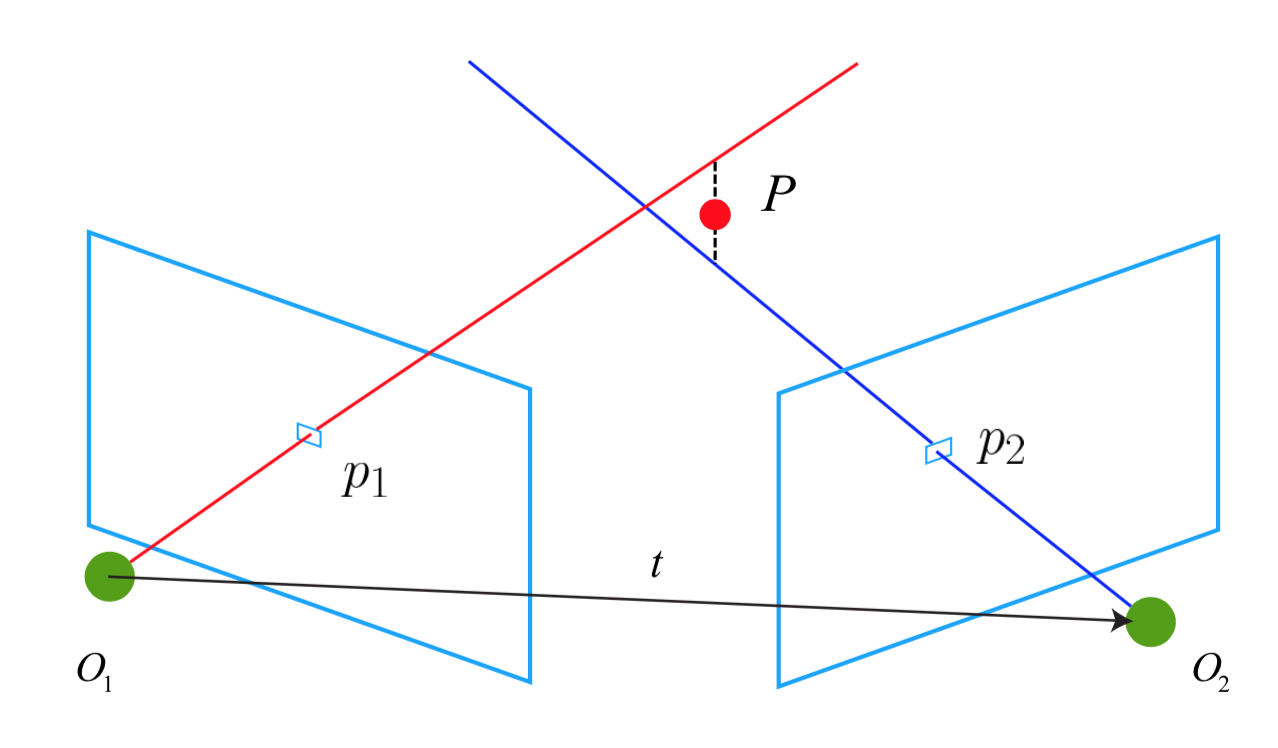
1 定义

已知两幅图像间的姿态 \(T=\left[\begin{array}{l}
\mathbf{r}_{1} \\
\mathbf{r}_{2} \\
\mathbf{r}_{3}
\end{array}\right]=[R \quad t]\) 和三维点在两幅图像上对应的匹配点 \(\boldsymbol{p}_1\) 和 \(\boldsymbol{p}_2\) （其归一化坐标为 \(x_{1}=\left(\begin{array}{c}
u_{1} \\
v_{1} \\
1
\end{array}\right)\), \(x_{2}=\left(\begin{array}{c}
u_{2} \\
v_{2} \\
1
\end{array}\right)\)）。希望求解点 \(P=\left[\begin{array}{l}
X \\
Y \\
Z \\
1
\end{array}\right]\) 的三维位置。

2 求解

本文主要求解推导参见这篇文章。

2.1 叉乘消元求解

设 \(x_{1}=\left(\begin{array}{c}
u_{1} \\
v_{1} \\
1
\end{array}\right)\), \(x_{2}=\left(\begin{array}{c}
u_{2} \\
v_{2} \\
1
\end{array}\right)\) 为两个特征点的归一化坐标，
按照对极约束 (Epipolar Constraint)中的定义：
\(s_{1} \boldsymbol{x}_{1}=s_{2} \boldsymbol{R} \boldsymbol{x}_{2}+\boldsymbol{t}\tag{1}\)

我们希望求解的是特征点的深度 \(\boldsymbol{s}_1\) 或者 \(\boldsymbol{s}_2\)。
对于公式 (1) 两边左乘 \(\boldsymbol{x}_{1}^{\wedge}\)：
\(s_{1} \boldsymbol{x}_{1}^{\wedge} \boldsymbol{x}_{1}=0=s_{2} \boldsymbol{x}_{1}^{\wedge} \boldsymbol{R} \boldsymbol{x}_{2}+\boldsymbol{x}_{1}^{\wedge} \boldsymbol{t}\tag{2}\)

但是由于噪声的存在，显然未必能够满足公式 (2) 等于0。因此最好的方式一般都是用最小二乘法。

2.2 线性方程求解

在 VINS-Mono 和 ORB-SLAM 中很多都用类似的求解线性方程的方法。它的大概思路如下：
定义三维点 \(P=\left[\begin{array}{l}
X \\
Y \\
Z \\
1
\end{array}\right]\)，其归一化坐标表示为 \(\mathbf{x}=\left[\begin{array}{l}
u \\
v \\
1
\end{array}\right]\)
根据投影方程：
\(\begin{aligned}
& \lambda \mathbf{x}=T P \\
&\Rightarrow \lambda \mathbf{x} \times T P=0 \\
&\Rightarrow \hat{\mathbf{x}} T P=0
\end{aligned}\tag{3}\)

利用向量叉乘的性质：
\(\mathbf{a} \times \mathbf{b}=\hat{\mathbf{a}} \mathbf{b}=\left[\begin{array}{ccc}
0 & -a_{3} & a_{2} \\
a_{3} & 0 & -a_{1} \\
-a_{2} & a_{1} & 0
\end{array}\right]\left[\begin{array}{l}
b_{1} \\
b_{2} \\
b_{3}
\end{array}\right]\tag{4}\)
其中 \(\hat{\mathbf{a}}\) 表示向量 \(\mathbf{a}\) 对应的 反对称矩阵 (Skew-symmetric Matrix)。
得到：
\(\begin{aligned}
\hat{\mathbf{x}} T P &=\left[\begin{array}{ccc}
0 & -1 & v \\
1 & 0 & -u \\
-v & u & 0
\end{array}\right]\left[\begin{array}{l}
\mathbf{r}_{1} \\
\mathbf{r}_{2} \\
\mathbf{r}_{3}
\end{array}\right] P \\
&=\left[\begin{array}{c}
-\mathbf{r}_{2}+v \mathbf{r}_{3} \\
\mathbf{r}_{1}-u \mathbf{r}_{\mathbf{3}} \\
-v \mathbf{r}_{1}+u \mathbf{r}_{2}
\end{array}\right] P
\end{aligned}\tag{5}\)

显然第一行 \(-\times \boldsymbol{u}\)、第二行 \(-\times \boldsymbol{v}\) 再相加即可得到第三行，所以是线性相关的，只需2个方程即可：
\(\left[\begin{array}{c}
-\mathbf{r}_{2}+v \mathbf{r}_{3} \\
\mathbf{r}_{1}-u \mathbf{r}_{3}
\end{array}\right] P=0\tag{6}\)

因此已知一个相机的观测可以得到两个方程组，要求的三维点包含3个变量，理论上只需要2个以上相机观测即可进行三角化。
\(\left[\begin{array}{c}
-\mathbf{r}_{2}^{(1)}+v^{(1)} \mathbf{r}_{3}^{(1)} \\
\mathbf{r}_{1}^{(1)}-u^{(1)} \mathbf{r}_{3}^{(1)} \\
-\mathbf{r}_{2}^{(2)}+v^{(2)} \mathbf{r}_{3}^{(2)} \\
\mathbf{r}_{\mathbf{1}}^{(2)}-u^{(2)} \mathbf{r}_{3}^{(2)} \\
\vdots
\end{array}\right] X=0\tag{7}\)

上述方程为超定方程没有非0解，适合使用 SVD 求最小二乘解。对于双视图问题，我们令：
\(\boldsymbol{A}=\left[\begin{array}{c}
-\mathbf{r}_{2}^{(1)}+v^{(1)} \mathbf{r}_{3}^{(1)} \\
\mathbf{r}_{1}^{(1)}-u^{(1)} \mathbf{r}_{3}^{(1)} \\
-\mathbf{r}_{2}^{(2)}+v^{(2)} \mathbf{r}_{3}^{(2)} \\
\mathbf{r}_{\mathbf{1}}^{(2)}-u^{(2)} \mathbf{r}_{3}^{(2)}
\end{array}\right]_{6 \times 4}\tag{8}\)

求解 \(\boldsymbol{A}x=0\) 就转化成如下问题：

\(J(x)=\min \|\boldsymbol{A} x\|\tag{9}\)

使用 SVD 分解 \(A=U D V^{T}\)，其中：\(U \in R^{6 \times 6}, D \in R^{6 \times 4}, V \in R^{4 \times 4}\)。由于 \(D \in R^{6 \times 4}\)，则最小值在 \(y=[0,0,0,1]^{T}\) 也就是 V 的最右列得到：
\(y=V^{T} x \Longrightarrow x=\left[\begin{array}{l}
x_0 \\
x_1 \\
x_2 \\
x_3
\end{array}\right]=V y\tag{10}\)

同时由于 \(P=\left[\begin{array}{l}
X \\
Y \\
Z \\
1
\end{array}\right]\) 为齐次坐标，因此进行如下处理使得最后一项为 1：
\(X=\left[\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right]=\left[\begin{array}{l}
x_{0} / x_{3} \\
x_{1} / x_{3} \\
x_{2} / x_{3} \\
x_{3} / x_{3}
\end{array}\right]\tag{11}\)

当然如果不是已知归一化平面坐标而是像素坐标 \(\mathbf{x}^{\prime}=\left[\begin{array}{l}
u^{\prime} \\
v^{\prime} \\
1
\end{array}\right]\) 和内参 K，也是一样的：
\(\begin{aligned}
& \lambda \mathrm{x}^{\prime}=K T P \\
\Rightarrow & \lambda \mathbf{x}^{\prime} \times K T P=0 \\
\Rightarrow & \hat{\mathbf{x}}^{\prime} K T P=0 \\
\Rightarrow & \hat{\mathbf{x}}^{\prime} H P=0
\end{aligned}\tag{12}\)
只不过系数矩阵由 T 变成了 \(H=K T\)

以下是 VINS-Mono 中的代码，使用 SVD 求解方程，和上面的过程是一样的：

参考材料

[1] https://www.cnblogs.com/FangLai-you/p/11276148.html
[2] https://www.cnblogs.com/Jessica-jie/p/7730731.html
[3] https://zhuanlan.zhihu.com/p/103694374
[4] 《视觉 SLAM 十四讲》
[5] https://blog.csdn.net/michaelhan3/article/details/89483148
[6] https://note.youdao.com/ynoteshare1/index.html?id=5e98f487c40ef22f90e1177f29271be5&type=note
[7] https://blog.csdn.net/weixin_43795395/article/details/95677116