施密特正交化 | Schmidt Orthogonalization

1 定义

施密特正交化（Schmidt orthogonalization）是求欧氏空间正交基的一种方法。从欧氏空间（\(\mathbb{R}^n\)）任意线性无关的向量组 \(\mathbf{v}_1，\mathbf{v}_2，\cdots，\mathbf{v}_{m}\) 出发，求得正交向量组 \(\mathbf{u}_1，\mathbf{u}_2，\cdots，\mathbf{u}_{m}\)，使由 \(\mathbf{v}_1，\mathbf{v}_2，\cdots，\mathbf{v}_{m}\) 与向量组 \(\mathbf{u}_1，\mathbf{u}_2，\cdots，\mathbf{u}_{m}\) 等价，再将正交向量组中每个向量经过单位化，就得到一个标准正交向量组，这种方法称为施密特正交化。

2 算法

记 \(S=\left\{\mathbf{v}_1, \ldots, \mathbf{v}_{m}\right\}\) 是某向量空间（\(\mathbb{R}^n\)）的基（其中 \(m \leq n\)）。由向量 \(\mathbf{v}_1, \ldots, \mathbf{v}_{m}\) 张成的子空间记为 \(\text{span}\left\{\mathbf{v}_1, \ldots, \mathbf{v}_{m}\right\}\)。

那么可通过下列做法找到该向量空间中的 \(n\) 个两两正交的向量 \(S^{\prime}=\left\{\mathbf{u}_1, \ldots, \mathbf{u}_m\right\}\)。该方法称为施密特正交化（Gram–Schmidt process）。

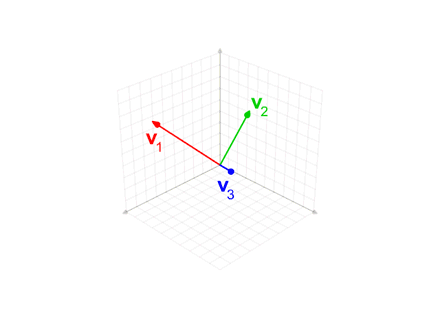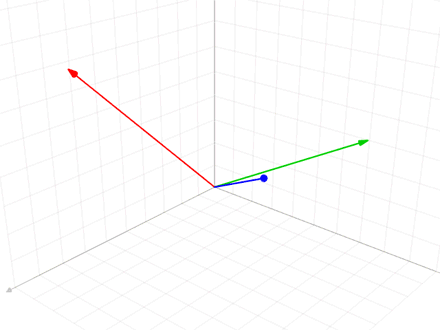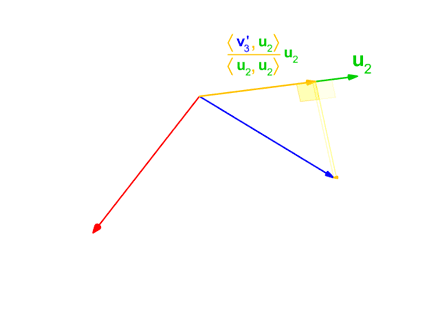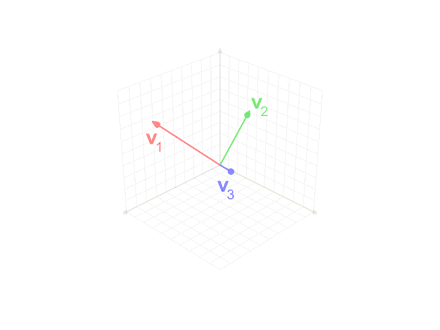
具体方法就是以某一个基向量作为初始，将另一个向量依次向其投影，投影操作公式为：
\(
\begin{equation}
\operatorname{proj}_{\mathbf{u}}(\mathbf{v})=\frac{\langle\mathbf{u}, \mathbf{v}\rangle}{\langle\mathbf{u}, \mathbf{u}\rangle} \mathbf{u}
\end{equation}
\)

其中 \(\mathbf{u} \neq 0\)，如果 \(\mathbf{u} = 0\) 则记为：
\(
\begin{equation}
\operatorname {proj} _{\mathbf {0} }(\mathbf {v} ):=\mathbf {0}
\end{equation}
\)

根据上述方式，施密特正交化（Gram–Schmidt process）计算过程如下：

\(
\begin{align}
\mathbf{u}_1 & = \mathbf{v}_1, & \mathbf{e}_1 & = \frac{\mathbf{u}_1}{\|\mathbf{u}_1\|} \\
\mathbf{u}_2 & = \mathbf{v}_2-\operatorname{proj}_{\mathbf{u}_1} (\mathbf{v}_2),
& \mathbf{e}_2 & = \frac{\mathbf{u}_2}{\|\mathbf{u}_2\|} \\
\mathbf{u}_3 & = \mathbf{v}_3-\operatorname{proj}_{\mathbf{u}_1} (\mathbf{v}_3) - \operatorname{proj}_{\mathbf{u}_2} (\mathbf{v}_3),
& \mathbf{e}_3 & = \frac{\mathbf{u}_3 }{\|\mathbf{u}_3\|} \\
\mathbf{u}_4 & = \mathbf{v}_4-\operatorname{proj}_{\mathbf{u}_1} (\mathbf{v}_4)-\operatorname{proj}_{\mathbf{u}_2} (\mathbf{v}_4)-\operatorname{proj}_{\mathbf{u}_3} (\mathbf{v}_4),
& \mathbf{e}_4 & = {\mathbf{u}_4 \over \|\mathbf{u}_4\|} \\
& {}\ \ \vdots & & {}\ \ \vdots \\
\mathbf{u}_{m} & = \mathbf{v}_{m} - \sum_{j=1}^{m-1}\operatorname{proj}_{\mathbf{u}_j} (\mathbf{v}_{m}),
& \mathbf{e}_{m} & = \frac{\mathbf{u}_{m}}{\|\mathbf{u}_{m}\|}.
\end{align}
\)

这样就得到了 \(\text{span}\left\{\mathbf{v}_1, \ldots, \mathbf{v}_{m}\right\}\) 上的一组正交基 \(\left\{\mathbf{u}_1, \ldots, \mathbf{u}_m\right\}\)，以及相应的标准正交基 \(\left\{\mathbf{e}_1, \ldots, \mathbf{e}_m\right\}\)。

参考材料

[1] https://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process
[2] https://www.matongxue.com/parts/4664/