特征值与特征向量 | Eigenvalue and Eigenvector

1 定义

设 \(A\) 是 \(n\) 阶方阵，如果存在常数及非零 \(n\) 向量 \(x\)，使得 \(Ax=\lambda x\)，则称是矩阵 \(A\) 的特征值，\(x\) 是 \(A\) 属于特征值的特征向量。

2 几何意义

矩阵的几何意义
一个矩阵代表的是一个线性变换规则，而一个矩阵的乘法运行代表的是一个变换。
例如矩阵：\(A=\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)\) 对列向量 \(x=\left(\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right)\) 进行线性变换就得到新的向量 \(y\)：
\(A x=\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)\left(\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right)=\left(\begin{array}{l}
a_{11} x_{1}+a_{12} x_{2} \\
a_{21} x_{1}+a_{22} x_{2}
\end{array}\right)=\left(\begin{array}{l}
y_{1} \\
y_{2}
\end{array}\right)=y\tag{1}\)
类似下图的演示：

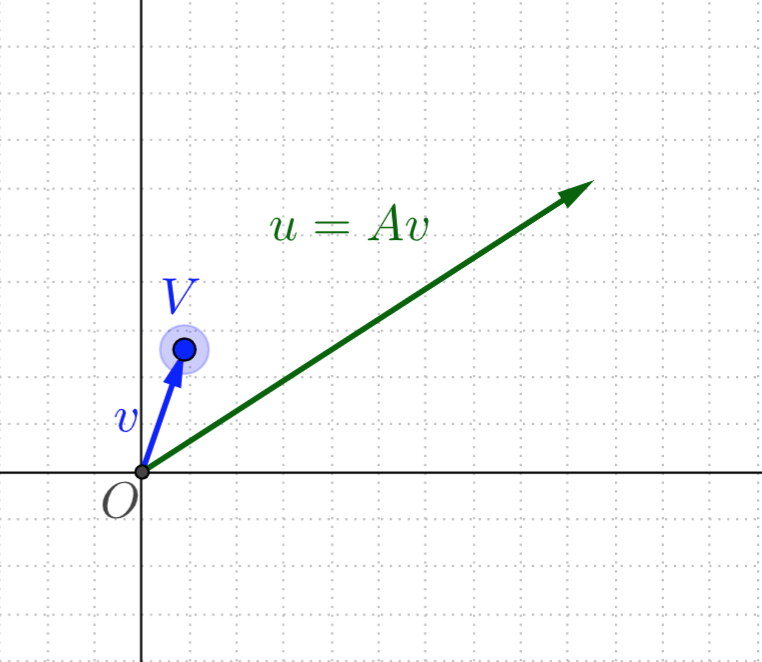
特征向量的几何意义
一个变换（或者说矩阵）的特征向量就是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已。
\(A x=\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)\left(\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right)=\left(\begin{array}{l}
a_{11} x_{1}+a_{12} x_{2} \\
a_{21} x_{1}+a_{22} x_{2}
\end{array}\right)=\left(\begin{array}{l}
\lambda x_{1} \\
\lambda x_{2}
\end{array}\right)=y\tag{2}\)

类似下图的演示：

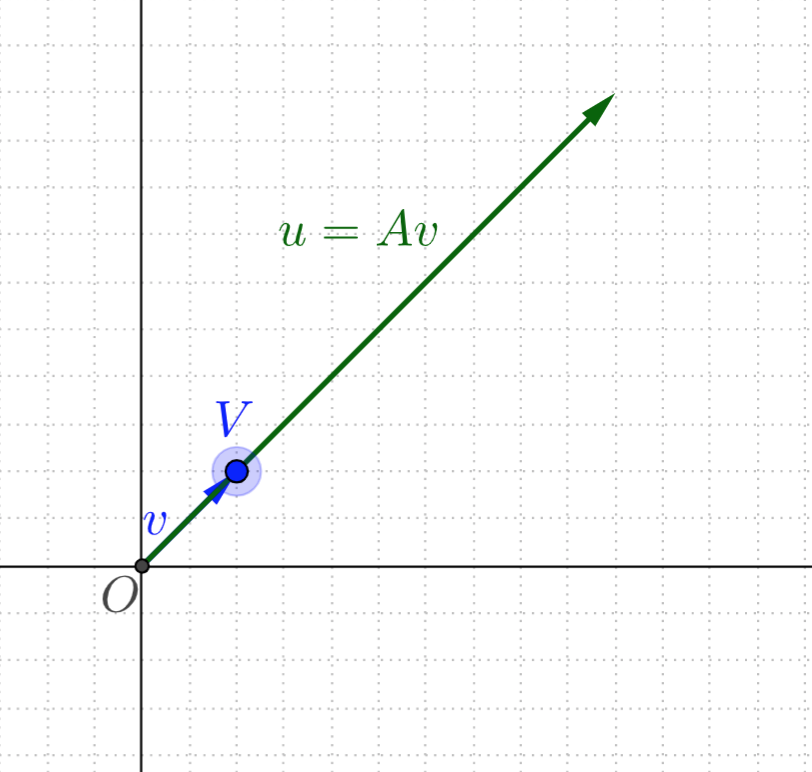
一个交互演示可以参见：https://www.geogebra.org/m/KuMAuEnd

3 求解

\(n\) 阶矩阵 \(A\) 的 \(n\) 个特征值，就是如下 特征方程 的 \(n\) 个跟 \(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\)。
\(|A-\lambda I|=0\tag{3}\)
而 \(A\) 属于特征值 \(\lambda_{i}\) 的特征向量就是如下线性方程的非零解：
\((A-\lambda I) \mathbf{x}=\mathbf{0}\tag{4}\)

4 性质

根据定义可以很容易推导 \(A^{2} \mathbf{x}=A(A \mathbf{x})=A(\lambda \mathbf{x})=\lambda(A \mathbf{x})=\lambda^{2} \mathbf{x}\)，进而得出下列性质：

• \(k A x=k \lambda x\)
• \(A^{k} \mathbf{x}=\lambda^{k} \mathbf{x}\)
• \(A^{-1} \mathbf{x}=1 / \lambda \mathbf{x}\)。其中 \(\lambda \neq 0\)
• \(e^{A t} \mathbf{x}=e^{\lambda t} \mathbf{x}\)。利用泰勒展开：\(e^{x}=\sum_{n=0}^{\infty} \frac{x^{n}}{n !}=1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}+\cdots\)

如果矩阵 \(A\) 有 \(n\) 个互不相关的特征向量 \(\)，则空间中任意向量可以用这 \(n\) 个特征向量作为基底表示为：
\(\mathbf{v}=c_{1} \mathbf{x}_{\mathbf{1}}+\cdots+c_{n} \mathbf{x}_{\mathbf{n}}\tag{5}\)

则有：
\(\begin{aligned}
A^{k} \mathbf{v} &=A^{k} c_{1} \mathbf{x}_{1}+\cdots+A^{k} c_{n} \mathbf{x}_{\mathbf{n}} \\
A&=c_{1} A^{k} \mathbf{x}_{1}+\cdots+c_{n} A^{k} \mathbf{x}_{\mathbf{n}} \\
&=c_{1} \lambda_{1}^{k} \mathbf{x}_{1}+\cdots+c_{n} \lambda_{n}^{k} \mathbf{x}_{\mathbf{n}}
\end{aligned}\tag{6}\)

5 矩阵的迹和行列式

矩阵的迹等于特征向量的和：
\(\operatorname{tr}(\mathbf{A})=\lambda_{1}+\lambda_{2}+\cdots+\lambda_{n}\tag{7}\)

矩阵的行列式等于特征向量的积：
\(\operatorname{det}(A)=\lambda_{1} \lambda_{2} \cdots \lambda_{n}\tag{8}\)

参考文献

[1] https://blog.csdn.net/weixin_37721518/article/details/79016226
[2] https://www.cnblogs.com/long5683/p/13142126.html
[3] https://zhuanlan.zhihu.com/p/111099659
[4] https://zhuanlan.zhihu.com/p/95836870
[5] https://jingyan.baidu.com/article/27fa7326afb4c146f8271ff3.html
[6] https://blog.csdn.net/qq_32294855/article/details/90114833
[7] https://www.geogebra.org/m/KuMAuEnd